Hooke’s Law and the Simple Harmonic Motion of a Spring

Introduction


To determine the force constant of a spring and to study the motion of a spring and mass
when vibrating under influence of gravity. When a spring is stretched a distance x from its equilibrium position, it will exert a restoring force directly proportional to this distance. We write this restoring force, F, as: F  =  -kx. where k is the spring constant and depends on the stiffness of the spring.  The minus
sign remind us that the direction of the force is opposite to the displacement.  Equation 1 is valid for most springs and is called Hooke’s Law. If a mass is attached to a spring that is hung vertically, and the mass is pulled down and released, the spring and the mass will oscillate about the original point of equilibrium. Using Newton’s second law and some calculus we can show that the motion is periodic (repeats itself over and over) and has period, T (in sec), given by  T =[(4pi^2)/k)m]^(1/2)

Calculations

 F  =  -kx


 T =[(4pi^2)/k)m]^(1/2)

Data

Mass (kg)	Force (N)	Initial (m)	Final (m)	Period (s)	Amplitude (m)	Frequency (Hz)	Period^2 (s)
0		0.177	0.277
0.35	-3.43	0.325	0.425	0.784	0.0895	1.276	0.5824
0.45	-4.41	0.369	0.469	0.884	0.0892	1.131	0.7488
0.55	-5.39	0.412	0.512	0.972	0.0857	1.029	0.9152
0.65	-6.37	0.452	0.552	1.056	0.1025	0.947	1.0816
0.75	-7.35	0.493	0.593	1.134	0.0891	0.882	1.2481
0.85	-8.33	0.538	0.638	1.21	0.0676	0.826	1.4145
0.95	-9.31	0.579	0.679	1.268	0.0887	0.789	1.5809
1.05	-10.29	0.618	0.718	1.346	0.0784	0.743	1.7473

 1050g Positon vs Time

Here is the postion vs time graph for the spring loaded with a mass of 1050g  with a sinusoidal fit

 350g Position vs Time

Here is the postion vs time graph for the spring loaded with a mass of 1050g 

Force vs Displacement of all Runs

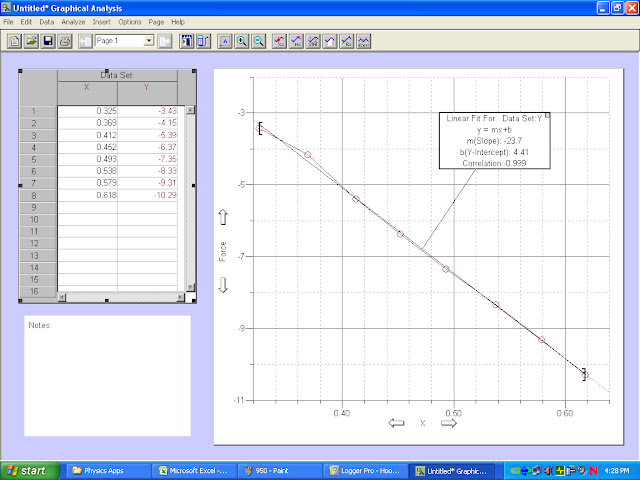This the Force vs Displacement graph for all of the runs 350g through 1050g

Conclusions
In this lab we went over Hooks law of springs. We learned how to find a spring constant (k) by having a known mass, a length of displacement of the spring. The spring is stretched and the mass is attached and let go for 10 seconds. The spring oscillates and the position vs time is recorded. the spring constant can be calculated using F=-kx